[LeetCode] 每日一题 July 1~10

  • July 1 - LCP 07. 传递信息；
  • July 2 - 1833. 雪糕的最大数量；
  • July 3 - 根据字符出现频率排序；
  • July 4 - 645. 错误的集合；
  • July 5 - 726. 原子的数量；
  • July 6 - 1418. 点菜展示表；
  • July 7 - 1711. 大餐计数；
  • July 8 - 930. 和相同的二元子数组；
  • July 9 - 面试题 17.10. 主要元素；
  • July 10 - 981. 基于时间的键值存储

July 1 - LCP 07. 传递信息

描述

小朋友 A 在和 ta 的小伙伴们玩传信息游戏，游戏规则如下：

  • 有 n 名玩家，所有玩家编号分别为 0 ～ n-1，其中小朋友 A 的编号为 0
  • 每个玩家都有固定的若干个可传信息的其他玩家（也可能没有）。传信息的关系是单向的（比如 A 可以向 B 传信息，但 B 不能向 A 传信息）。
  • 每轮信息必须需要传递给另一个人，且信息可重复经过同一个人

给定总玩家数 n，以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数；若不能到达，返回 0。

样例

1
2
3
输入：n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3
输出：3
说明：信息从小 A 编号 0 处开始，经 3 轮传递，到达编号 4。共有 3 种方案，分别是 0->2->0->4， 0->2->1->4， 0->2->3->4
1
2
输入：n = 3, relation = [[0,2],[2,1]], k = 2
输出：0
1
2
3
4
5
限制：
    2 <= n <= 10
	1 <= k <= 5
	1 <= relation.length <= 90, 且 relation[i].length == 2
	0 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]

思路

方法一：深度优先搜索

可以把传信息的关系看成有向图，每个玩家对应一个节点，每个传信息的关系对应一条有向边。如果 x 可以向 y 传信息，则对应从节点 x 到节点 y 的一条有向边。寻找从编号 0 的玩家经过 k 轮传递到编号 n−1 的玩家处的方案数，等价于在有向图中寻找从节点 0 到节点 n−1 的长度为 k 的路径数，同一条路径可以重复经过同一个节点。

可以使用深度优先搜索计算方案数。从节点 0 出发做深度优先搜索，每一步记录当前所在的节点以及经过的轮数，当经过 k 轮时，如果位于节点 n−1，则将方案数加 1。搜索结束之后，即可得到总的方案数。

时间复杂度：O(n^k)。最多需要遍历 k 层，每层遍历最多有 O(n) 个分支。

空间复杂度：O(n+m+k)。其中 m 为 relation 数组的长度。空间复杂度主要取决于图的大小和递归调用栈的深度，保存有向图信息所需空间为 O(n+m)，递归调用栈的深度不会超过 k。

方法二：广度优先搜索

也可以使用广度优先搜索计算方案数。从节点 0 出发做广度优先搜索，当遍历到 k 层时，如果位于节点 n−1，则将方案数加 1。搜索结束之后，即可得到总的方案数。

方法三：动态规划

这道题是计数问题，可以使用动态规划的方法解决。

定义动态规划的状态 dp[i][j]为经过 i 轮传递到编号 j 的玩家的方案数，其中 0≤i≤k，0≤j<n。

由于从编号 0 的玩家开始传递，当 i=0 时，一定位于编号 0 的玩家，不会传递到其他玩家，因此动态规划的边界情况如下：

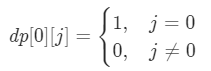
对于传信息的关系 [src,dst]，如果第 i轮传递到编号 src 的玩家，则第 i+1 轮可以从编号 src 的玩家传递到编号 dst 的玩家。因此在计算 dp[i+1][dst] 时，需要考虑可以传递到编号 dst 的所有玩家。由此可以得到动态规划的状态转移方程，其中 0≤i<k：

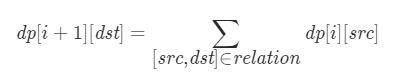
最终得到 dp[k][n−1] 即为总的方案数。

时间复杂度：O(km)。其中 m为 relation 数组的长度。

空间复杂度是 O(kn)。由于当 i>0 时，dp[i][] 的值只和dp[i−1][] 的值有关，因此可以将二维数组变成一维数组，将空间复杂度优化到 O(n)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//动态规划
class Solution {
public:
    int numWays(int n, vector<vector<int>>& relation, int k) {
        vector<vector<int>> dp(k + 1, vector<int>(n));
        dp[0][0] = 1;
        for (int i = 0; i < k; i++) {
            for (auto& edge : relation) {
                int src = edge[0], dst = edge[1];
                dp[i + 1][dst] += dp[i][src];
            }
        }
        return dp[k][n - 1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//动态规划空间复杂度优化
class Solution {
public:
    int numWays(int n, vector<vector<int>>& relation, int k) {
        vector<int> dp(n);
        dp[0] = 1;
        for (int i = 0; i < k; i++) {
            vector<int> next(n);
            for (auto& edge : relation) {
                int src = edge[0], dst = edge[1];
                next[dst] += dp[src];
            }
            dp = next;
        }
        return dp[n - 1];
    }
};

参考

C++ vector 容器浅析 | 菜鸟教程 (runoob.com)

July 2 - 1833. 雪糕的最大数量

描述

商店中新到 n 支雪糕，用长度为 n 的数组 costs 表示雪糕的定价，其中 costs[i] 表示第 i 支雪糕的现金价格。Tony 一共有 coins 现金可以用于消费，他想要买尽可能多的雪糕。

给你价格数组 costs 和现金量 coins ，请你计算并返回 Tony 用 coins 现金能够买到的雪糕的 最大数量 。

思路

排序 + 贪心

对数组costs 排序，然后按照从小到大的顺序遍历数组元素，对于每个元素，如果该元素不超过剩余的硬币数，则将硬币数减去该元素值，表示购买了这支雪糕，当遇到一个元素超过剩余的硬币数时，结束遍历，此时购买的雪糕数量即为可以购买雪糕的最大数量。

时间复杂度：O(nlogn)，其中 n 是数组 costs 的长度。对数组排序的时间复杂度是 O(nlogn)，遍历数组的时间复杂度是O(n)，因此总时间复杂度是O(nlogn)。

空间复杂度：O(logn)，其中 n 是数组 costs 的长度。空间复杂度主要取决于排序使用的额外空间。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxIceCream(vector<int>& costs, int coins) {
        int i=0;
        sort(costs.begin(),costs.end());
        for(auto &a : costs){
            if(a<=coins){
                i++;
                coins-=a;
            }
            else{
                break;
            }
        }
        return i;
    }
};

July 3 - 根据字符出现频率排序

描述

给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

样例

1
2
3
4
5
6
7
8
9
输入:
"tree"

输出:
"eert"

解释:
'e'出现两次，'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外，"eetr"也是一个有效的答案。
1
2
3
4
5
6
7
8
9
输入:
"Aabb"

输出:
"bbAa"

解释:
此外，"bbaA"也是一个有效的答案，但"Aabb"是不正确的。
注意'A'和'a'被认为是两种不同的字符。

思路

题目要求将给定的字符串按照字符出现的频率降序排序，因此需要首先遍历字符串，统计每个字符出现的频率，然后每次得到频率最高的字符，生成排序后的字符串。

可以使用哈希表记录每个字符出现的频率，将字符去重后存入列表，再将列表中的字符按照频率降序排序。

生成排序后的字符串时，遍历列表中的每个字符，则遍历顺序为字符按照频率递减的顺序。对于每个字符，将该字符按照出现频率拼接到排序后的字符串。例如，遍历到字符 c，该字符在字符串中出现了 freq 次，则将 freq 个字符 c 拼接到排序后的字符串。

时间复杂度：O(n+klogk)，其中 n 是字符串 s 的长度，k 是字符串 s 包含的不同字符的个数，这道题中 s 只包含大写字母、小写字母和数字，因此 k=26+26+10=62。遍历字符串统计每个字符出现的频率需要 O(n) 的时间。将字符按照出现频率排序需要 O(klogk) 的时间。生成排序后的字符串，需要遍历 k 个不同字符，需要 O(k) 的时间，拼接字符串需要 O(n) 的时间。因此总时间复杂度是 O(n+klogk+k+n)=O(n+klogk)。

空间复杂度：O(n+k)，其中 n 是字符串 s 的长度，k 是字符串 s 包含的不同字符的个数。空间复杂度主要取决于哈希表、列表和生成的排序后的字符串。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    static bool cmp(pair<char,int>a, pair<char,int>b){
        return a.second > b.second;
    }

    string frequencySort(string s) {
        unordered_map<char,int>freq;
        for(auto m:s){
            freq[m]++;
        }
        vector<pair<char,int>>vec;
        for(auto n:freq){
            vec.push_back(n);
        }
        sort(vec.begin(),vec.end(),cmp);
        string result;
        for(auto k:vec){
            for(int i=0;i<k.second;i++){
                result.push_back(k.first);
            }
        }
        return result;
    }
};

问题

reference to non-static member function must be called

错误：reference to non-static member function must be called_initHeart的博客-CSDN博客

恼人的函数指针（二）：指向类成员的指针 - AnnieKim - 博客园 (cnblogs.com)

参考

C++中 sort() 的使用_LucienShui-CSDN博客

C++ pair的基本用法总结（整理）_sevenjoin的博客-CSDN博客_c++ pair

关联容器：unordered_map详细介绍（附可运行代码）_Voidsky-CSDN博客

C++ STL vector添加元素（push_back()和emplace_back()）详解 (biancheng.net)

July 4 - 645. 错误的集合

描述

集合 s 包含从 1 到 n 的整数。不幸的是，因为数据错误，导致集合里面某一个数字复制了成了集合里面的另外一个数字的值，导致集合 丢失了一个数字 并且 有一个数字重复 。

给定一个数组 nums 代表了集合 S 发生错误后的结果。

请你找出重复出现的整数，再找到丢失的整数，将它们以数组的形式返回。

样例

1
2
输入：nums = [1,2,2,4]
输出：[2,3]
1
2
输入：nums = [1,1]
输出：[1,2]
1
2
输入：nums = [3,2,3,4,6,5]
输出：[3,1]
1
2
输入：nums = [1,5,3,2,2,7,6,4,8,9]
输出：[2,10]

思路

方法一：排序

将数组排序之后，比较每对相邻的元素，即可找到错误的集合。

寻找重复的数字较为简单，如果相邻的两个元素相等，则该元素为重复的数字。

寻找丢失的数字相对复杂，可能有以下两种情况：

  • 如果丢失的数字大于 1 且小于 n，则一定存在相邻的两个元素的差等于 2，这两个元素之间的值即为丢失的数字；
  • 如果丢失的数字是 1 或 n，则需要另外判断。

时间复杂度：O(nlogn)，其中 nn 是数组 nums 的长度。排序需要 O(nlogn) 的时间，遍历数组找到错误的集合需要 O(n) 的时间，因此总时间复杂度是 O(nlogn)。

空间复杂度：O(logn)，其中 n 是数组 nums 的长度。排序需要 O(logn) 的空间。

方法二：哈希表

重复的数字在数组中出现 2 次，丢失的数字在数组中出现 0 次，其余的每个数字在数组中出现 1 次。因此可以使用哈希表记录每个元素在数组中出现的次数，然后遍历从 1 到 n 的每个数字，分别找到出现 2 次和出现 0 次的数字，即为重复的数字和丢失的数字。

时间复杂度：O(n)，其中 n 是数组 nums 的长度。需要遍历数组并填入哈希表，然后遍历从 1 到 n 的每个数寻找错误的集合。

空间复杂度：O(n)，其中 n 是数组nums 的长度。需要创建大小为 O(n) 的哈希表。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//方法1，排序
class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        vector<int> result(2);
        sort(nums.begin(), nums.end());
        int prev = 0;
        int n = nums.size();
        for(int i=0; i<nums.size(); i++){
            int curr = nums[i];
            if(curr == prev){
                result[0] = prev;
            }
            else if(curr - prev > 1){
                result[1] = curr - 1;
            }
            prev = curr;
        } 
        if(nums[n-1] != n){
            result[1] = n;
        }       
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//方法2，hash表
class Solution {
public:
    vector<int> findErrorNums(vector<int>& nums) {
        vector<int> result(2);
        int n = nums.size();
        unordered_map<int,int>num_map;
        for(auto i:nums){
            num_map[i]++;
        }
        for(int j=1; j<=n; j++){
            if(num_map[j] == 0){
                result[1] = j;
            }
            else if(num_map[j] == 2){
                result[0] = j;
            }
        }
        return result;
    }
};

问题

  • 注意数组边界，前后两个数字相比时，注意后面一个数字不要越界
  • 注意特殊情况，当缺少1或者n时的特殊处理

July 5 - 726. 原子的数量

July 6 - 1418. 点菜展示表

描述

给你一个数组 orders，表示客户在餐厅中完成的订单，确切地说， orders[i]=[customerNamei,tableNumberi,foodItemi] ，其中 customerNamei 是客户的姓名，tableNumberi 是客户所在餐桌的桌号，而 foodItemi 是客户点的餐品名称。

请你返回该餐厅的 点菜展示表 。在这张表中，表中第一行为标题，其第一列为餐桌桌号 “Table” ，后面每一列都是按字母顺序排列的餐品名称。接下来每一行中的项则表示每张餐桌订购的相应餐品数量，第一列应当填对应的桌号，后面依次填写下单的餐品数量。

注意：客户姓名不是点菜展示表的一部分。此外，表中的数据行应该按餐桌桌号升序排列。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
public:
    vector<vector<string>> displayTable(vector<vector<string>> &orders) {
        // 从订单中获取餐品名称和桌号，统计每桌点餐数量
        unordered_set<string> nameSet;
        unordered_map<int, unordered_map<string, int>> foodsCnt;
        for (auto &order : orders) {
            nameSet.insert(order[2]);
            int id = stoi(order[1]);
            ++foodsCnt[id][order[2]];
        }

        // 提取餐品名称，并按字母顺序排列
        int n = nameSet.size();
        vector<string> names;
        for (auto &name : nameSet) {
            names.push_back(name);
        }
        sort(names.begin(), names.end());

        // 提取桌号，并按餐桌桌号升序排列
        int m = foodsCnt.size();
        vector<int> ids;
        for (auto &[id, _] : foodsCnt) {
            ids.push_back(id);
        }
        sort(ids.begin(), ids.end());

        // 填写点菜展示表
        vector<vector<string>> table(m + 1, vector<string>(n + 1));
        table[0][0] = "Table";
        copy(names.begin(), names.end(), table[0].begin() + 1);
        for (int i = 0; i < m; ++i) {
            int id = ids[i];
            auto &cnt = foodsCnt[id];
            table[i + 1][0] = to_string(id);
            for (int j = 0; j < n; ++j) {
                table[i + 1][j + 1] = to_string(cnt[names[j]]);
            }
        }
        return table;
    }
};

July 7 - 1711. 大餐计数

描述

大餐 是指 恰好包含两道不同餐品 的一餐，其美味程度之和等于 2 的幂。

你可以搭配 任意 两道餐品做一顿大餐。

给你一个整数数组 deliciousness ，其中 deliciousness[i] 是第 i 道餐品的美味程度，返回你可以用数组中的餐品做出的不同 大餐 的数量。结果需要对 109 + 7 取余。

注意，只要餐品下标不同，就可以认为是不同的餐品，即便它们的美味程度相同。

样例

1
2
3
4
输入：deliciousness = [1,3,5,7,9]
输出：4
解释：大餐的美味程度组合为 (1,3) 、(1,7) 、(3,5) 和 (7,9) 。
它们各自的美味程度之和分别为 4 、8 、8 和 16 ，都是 2 的幂。
1
2
3
输入：deliciousness = [1,1,1,3,3,3,7]
输出：15
解释：大餐的美味程度组合为 3 种 (1,1) ，9 种 (1,3) ，和 3 种 (1,7) 。

思路

朴素的解法是遍历数组 deliciousness 中的每对元素，对于每对元素，计算两个元素之和是否等于 2 的幂。该解法的时间复杂度为 O(n^2)，会超出时间限制。

上述朴素解法存在同一个元素被重复计算的情况，因此可以使用哈希表减少重复计算，降低时间复杂度。具体做法是，使用哈希表存储数组中的每个元素的出现次数，遍历到数组 deliciousness 中的某个元素时，在哈希表中寻找与当前元素的和等于 2 的幂的元素个数，然后用当前元素更新哈希表。由于遍历数组时，哈希表中已有的元素的下标一定小于当前元素的下标，因此任意一对元素之和等于 2 的幂的元素都不会被重复计算。

令 maxVal 表示数组 deliciousness 中的最大元素，则数组中的任意两个元素之和都不会超过 maxVal×2。令 maxSum=maxVal×2，则任意一顿大餐的美味程度之和为不超过 maxSum 的某个 2 的幂。

对于某个特定的 2 的幂 sum，可以在 O(n) 的时间内计算数组 deliciousness 中元素之和等于 sum 的元素对的数量。数组 deliciousness 中的最大元素 maxVal 满足 maxVal≤C，其中 C=2^20，则不超过 maxSum 的 2 的幂有 O(logmaxSum)=O(logmaxVal)=O(logC) 个，因此可以在 O(nlogC) 的时间内计算数组 deliciousness 中的大餐数量。

时间复杂度：O(nlogC)，其中 n 是数组 deliciousness 的长度，C 是数组 deliciousness 中的元素值上限，这道题中 C=2^20 。需要遍历数组 deliciousness 一次，对于其中的每个元素，需要 O(logC) 的时间计算包含该元素的大餐数量，因此总时间复杂度是 O(nlogC)。

空间复杂度：O(n)，其中 n 是数组 deliciousness 的长度。需要创建哈希表，哈希表的大小不超过 n。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int countPairs(vector<int>& deliciousness) {
        int MOD = 1000000007;
        int result = 0;
        int maxVal =  *max_element(deliciousness.begin(),deliciousness.end());  
        int maxSum = maxVal * 2;
        unordered_map<int,int>map;
        for(auto a:deliciousness){
            for(int sum=1; sum<=maxSum; sum*=2){
                int num = map.count(sum-a)? map[sum-a]:0;
                result = (result + num) % MOD;
            }
            map[a]++;
        }
        return result;
    }
};

参考

July 8 - 930. 和相同的二元子数组

描述

给你一个二元数组 nums ，和一个整数 goal ，请你统计并返回有多少个和为 goal 的 非空 子数组。

子数组 是数组的一段连续部分。

样例

1
2
3
输入：nums = [1,0,1,0,1], goal = 2
输出：4
解释：有 4 个满足题目要求的子数组：[1,0,1]、[1,0,1,0]、[0,1,0,1]、[1,0,1]
1
2
输入：nums = [0,0,0,0,0], goal = 0
输出：15

思路

方法一：哈希表

假设原数组的前缀和数组为 sum，且子数组 (i,j] 的区间和为 goal，那么 sum[j]−sum[i]=goal。因此我们可以枚举 j ，每次查询满足该等式的 i 的数量。

具体地，我们用哈希表记录每一种前缀和出现的次数，假设我们当前枚举到元素 nums[j]，我们只需要查询哈希表中元素 sum[j]−goal 的数量即可，这些元素的数量即对应了以当前 j 值为右边界的满足条件的子数组的数量。最后这些元素的总数量即为所有和为 goal 的子数组数量。

在实际代码中，我们实时地更新哈希表，以防止出现 i≥j 的情况。

时间复杂度：O(n)，其中 n 为给定数组的长度。对于数组中的每个元素，我们至多只需要插入到哈希表中中一次。

空间复杂度：O(n)，其中 n 为给定数组的长度。哈希表中至多只存储 O(n) 个元素。

方法二：滑动窗口

注意到对于方法一中每一个 j，满足 sum[j]−sum[i]=goal 的 i 总是落在一个连续的区间中，i 值取区间中每一个数都满足条件。并且随着 j 右移，其对应的区间的左右端点也将右移，这样我们即可使用滑动窗口解决本题。

具体地，我们令滑动窗口右边界为 right，使用两个左边界 left1 和 left2 表示左区间 [left1 ,left2)，此时有 left2−left1 个区间满足条件。

在实际代码中，我们需要注意 left1≤left2≤right+1，因此需要在代码中限制 left1和 left2 不超出范围。

时间复杂度：O(n)，其中 n 为给定数组的长度。我们至多只需要遍历一次该数组。

空间复杂度：O(1)，我们只需要常数的空间保存若干变量。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//方法一：哈希表
class Solution {
public:
    int numSubarraysWithSum(vector<int>& nums, int goal) {
        int sum = 0;
        unordered_map<int,int>map;
        int result = 0;
        for(auto a:nums){
            map[sum]++;
            sum += a;
            result += map[sum-goal];
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//方法二：滑动窗口
class Solution {
public:
    int numSubarraysWithSum(vector<int>& nums, int goal) {
        int n = nums.size();
        int left1 = 0, left2 = 0, right = 0;
        int sum1 = 0, sum2 = 0;
        int ret = 0;
        while (right < n) {
            sum1 += nums[right];
            while (left1 <= right && sum1 > goal) {
                sum1 -= nums[left1];
                left1++;
            }
            sum2 += nums[right];
            while (left2 <= right && sum2 >= goal) {
                sum2 -= nums[left2];
                left2++;
            }
            ret += left2 - left1;
            right++;
        }
        return ret;
    }
};

July 9 - 面试题 17.10. 主要元素

描述

数组中占比超过一半的元素称之为主要元素。给你一个 整数 数组，找出其中的主要元素。若没有，返回 -1 。请设计时间复杂度为 O(N) 、空间复杂度为 O(1) 的解决方案。

样例

1
2
输入：[1,2,5,9,5,9,5,5,5]
输出：5
1
2
输入：[3,2]
输出：-1
1
2
输入：[2,2,2,3,3,4,4]
输出：-1 (元素2的个数没有超过一半)

思路

由于题目要求时间复杂度 O(n) 和空间复杂度 O(1)，因此符合要求的解法只有 Boyer-Moore 投票算法。

Boyer-Moore 投票算法的基本思想是：在每一轮投票过程中，从数组中删除两个不同的元素，直到投票过程无法继续，此时数组为空或者数组中剩下的元素都相等。

如果数组为空，则数组中不存在主要元素；

如果数组中剩下的元素都相等，则数组中剩下的元素可能为主要元素。

Boyer-Moore 投票算法的步骤如下：

维护一个候选主要元素 candidate 和候选主要元素的出现次数 count，初始时 candidate 为任意值，count=0；

遍历数组 nums 中的所有元素，遍历到元素 x 时，进行如下操作：

如果 count=0，则将 x 的值赋给 candidate，否则不更新 candidate 的值；

如果 x=candidate，则将 count 加 1，否则将 count 减 1。

遍历结束之后，如果数组 nums 中存在主要元素，则 candidate 即为主要元素，否则 candidate 可能为数组中的任意一个元素。

由于不一定存在主要元素，因此需要第二次遍历数组，验证 candidate 是否为主要元素。第二次遍历时，统计 candidate 在数组中的出现次数，如果出现次数大于数组长度的一半，则 candidate 是主要元素，返回 candidate，否则数组中不存在主要元素，返回 −1。

为什么当数组中存在主要元素时，Boyer-Moore 投票算法可以确保得到主要元素？

在 Boyer-Moore 投票算法中，遇到相同的数则将 count 加 1，遇到不同的数则将 count 减 1。根据主要元素的定义，主要元素的出现次数大于其他元素的出现次数之和，因此在遍历过程中，主要元素和其他元素两两抵消，最后一定剩下至少一个主要元素，此时 candidate 为主要元素，且 count≥1。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//普通解法O(n),O(n)
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int,int>map;
        int max = nums.size()/2;
        int result = -1;
        if(nums.size() == 1){
            return nums[0];
        }
        for(auto &a:nums){
            map[a]++;
            if(map[a] > max){
                result = a;
                max = map[a];
            }
        }
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//Boyer-Moore 投票算法 O(n),O(1)
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int candidate = -1;
        int count = 0;
        for(auto a:nums){
            if((count==0)&&(a!=candidate)){
                candidate=a;
                count++;
            }
            else if(a == candidate){
                count++;
            }
            else{
                count--;
            }
        }
        count = 0;
        for(auto b:nums){
            if(b==candidate){
                count++;
            }
        }
        if(count>nums.size()/2){
            return candidate;
        }
        else{
            return -1;
        }
    }
};

参考

主要元素 - 主要元素 - 力扣（LeetCode） (leetcode-cn.com)

July 10 - 981. 基于时间的键值存储

描述

创建一个基于时间的键值存储类 TimeMap，它支持下面两个操作：

  1. set(string key, string value, int timestamp)

    • 存储键 key、值 value，以及给定的时间戳 timestamp。

  2. get(string key, int timestamp)

    • 返回先前调用 set(key, value, timestamp_prev) 所存储的值，其中 timestamp_prev <= timestamp。
    • 如果有多个这样的值，则返回对应最大的 timestamp_prev 的那个值。
    • 如果没有值，则返回空字符串（””）。

样例

1
2
3
4
5
6
7
8
9
10
输入：inputs = ["TimeMap","set","get","get","set","get","get"], inputs = [[],["foo","bar",1],["foo",1],["foo",3],["foo","bar2",4],["foo",4],["foo",5]]
输出：[null,null,"bar","bar",null,"bar2","bar2"]
解释：  
TimeMap kv;   
kv.set("foo", "bar", 1); // 存储键 "foo" 和值 "bar" 以及时间戳 timestamp = 1   
kv.get("foo", 1);  // 输出 "bar"   
kv.get("foo", 3); // 输出 "bar" 因为在时间戳 3 和时间戳 2 处没有对应 "foo" 的值，所以唯一的值位于时间戳 1 处（即 "bar"）   
kv.set("foo", "bar2", 4);   
kv.get("foo", 4); // 输出 "bar2"   
kv.get("foo", 5); // 输出 "bar2"  
1
2
输入：inputs = ["TimeMap","set","set","get","get","get","get","get"], inputs = [[],["love","high",10],["love","low",20],["love",5],["love",10],["love",15],["love",20],["love",25]]
输出：[null,null,null,"","high","high","low","low"]
1
提示：所有 TimeMap.set 操作中的时间戳 timestamps 都是严格递增的。

思路

哈希表 + 二分查找

为实现 get 操作，我们需要用一个哈希表存储 set 操作传入的数据。具体地，哈希表的键为字符串 key，值为一个二元组列表，二元组中存储的是时间戳 timestamp 和值 value。

由于 set 操作中的时间戳都是严格递增的，因此二元组列表中保存的时间戳也是严格递增的，这样我们可以根据 get 操作中的 key 在哈希表中找到对应的二元组列表 pairs，然后根据 timestamp 在 pairs 中二分查找。我们需要找到最大的不超过 timestamp 的时间戳，对此，我们可以二分找到第一个超过 timestamp 的二元组下标 i，若 i>0 则说明目标二元组存在，即 pairs[i−1]，否则二元组不存在，返回空字符串。

时间复杂度：

  • 初始化 TimeMap 和 set 操作均为 O(1)；
  • get 操作为 O(logn)，其中 n 是 set 操作的次数。最坏情况下 set 操作插入的 key 均相同，这种情况下 get 中二分查找的次数为 O(logn)。

空间复杂度：O(n)，其中 n 是 set 操作的次数。我们需要使用哈希表保存每一次 set 操作的信息。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class TimeMap {
    unordered_map<string, vector<pair<int, string>>> m;

public:
    TimeMap() {}

    void set(string key, string value, int timestamp) {
        m[key].emplace_back(timestamp, value);
    }

    string get(string key, int timestamp) {
        auto &pairs = m[key];
        // 使用一个大于所有 value 的字符串
        // 以确保在 pairs 中含有 timestamp 的情况下也返回大于 timestamp 的位置
        pair<int, string> p = {timestamp, string({127})};
        auto i = upper_bound(pairs.begin(), pairs.end(), p);
        if (i != pairs.begin()) {
            return (i - 1)->second;
        }
        return "";
    }
};